Least Squares: fitting a line to a sequence of 2d-points

Version: 5.2.1

Least Squares: fitting a line to a sequence of 2d-points

(require (planet dyoo/least-squares:1:=3))

This is a simple implementation of the least squares method for lines, described in a standard statistics textbook [larsen2006]. Given a sequence of 2d-points, this library computes the slope and intersect of a line that best fits those points.

Here’s a quick-and-dirty example that shows how to use this package with a tool like Racket’s plot graph-plotting libraries:

> (require (planet dyoo/least-squares))
> (define data '(#(2.745 2.08) #(2.7 2.045) #(2.69 2.05)
                 #(2.68 2.005) #(2.675 2.035) #(2.67 2.035)
                 #(2.665 2.02) #(2.66 2.005) #(2.655 2.01)
                 #(2.655 2.0) #(2.65 2.0) #(2.65 2.005)
                 #(2.645 2.015) #(2.635 1.99) #(2.63 1.99)
                 #(2.625 1.995) #(2.625 1.985) #(2.62 1.97)
                 #(2.615 1.985) #(2.615 1.99) #(2.615 1.995)
                 #(2.61 1.99) #(2.59 1.975) #(2.59 1.995)
                 #(2.565 1.955)))
> (require plot)
> (plot (list (points data)
              (function (least-squares-function data))))

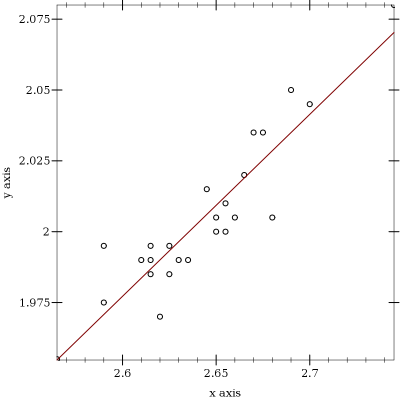
One of the more direct ways to use the library is to get the slope and intersect with least-squares:

> (define-values (a-slope an-intersect)
(least-squares '((0 -0.2342) (1 1.0001) (2 1.82123) (3 3.1415926))))
> a-slope
1.0948507800000002
> an-intersect
-0.2100955200000003

You can also use least-squares-function to probe the points on the fitted line:

> (define my-linear-function
(least-squares-function '((0 -0.2342) (1 1.0001) (2 1.82123) (3 3.1415926))))
> (my-linear-function 1)
0.8847552599999999
> (my-linear-function 2)
1.9796060400000002
> (my-linear-function 314)
343.5730494000001

1 API

(least-squares data) →
[slope number] [intersect number]
data :
(sequenceof (or/c (sequence number number)
posn))

Computes the slope and intersect for a line that best fits the points according to the method of least squares and returns them as two values.

For example:

> (define-values (a-slope an-intersect)
(least-squares '((2.718 3.1415926) (1.618 1.414213))))
> a-slope
1.5703450909090884
> an-intersect
-1.1266053570909036

(least-squares-function data) → [f (number -> number)]
data :
(sequenceof (or/c (sequence number number)
posn))

Constructs a function that fits the given data. For example:

> (define g
(least-squares-function '((2.718 3.1415926) (1.618 1.414213))))
> (g 0)
-1.1266053570909036
> (g 3)
3.584429915636362
> (g 27)
41.27271209745448

The function returned from least-squares-function is actually a structured value whose slope and intersect can be queried with least-squares-function-slope and least-squares-function-intersect.

(least-squares-function-slope f) → number
f : least-squares-function?

(least-squares-function-intersect f) → number
f : least-squares-function?

Example:

> (define h
(least-squares-function '((2.718 3.1415926) (1.618 1.414213))))
> (least-squares-function-slope h)
1.5703450909090884
> (least-squares-function-intersect h)
-1.1266053570909036

(least-squares-function? x) → boolean
x : any

Returns true if x is a function produced by least-squares-function. Example:

> (least-squares-function? (lambda (x) x))
#f
> (define k (least-squares-function '((0 0) (1 1))))
> (least-squares-function? k)
#t

Bibliography

[larsen2006] Richard J. Larsen and Morris L. Marx, An Introduction to Mathematical Statistics and Its Applications, 4th Edition. 2006.