Chebyshev Approximations
This chapter describes the routines for computing Chebyshev approximations to univariate functions provided by the PLT Scheme Science Collection. A Chebyshev approximation is a trucvation of the series
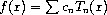
where the Chebyshev polymonials Tn(x) = cos(n arccos x) provides an orthogonal basis of polynomials in the interval [ - 1,1] with the weight function 1 / (1 - x2)1/2. The first few Chebyshev ploymonials are, T0(x) = 1, T1(x) = x, T2(x) = 2 x2 - 1. For more information see Abramowitz and Stegan, Chapter 22.
The functions described in this chapter are defined in the chebyshev.ss file in the science collection and are made available using the form:
(require (planet "chebyshev.ss" ("williams" "science.plt")))
11.1 The chebyshev-series Structure
Structure:
chebyshev-series |
|
Contract: (struct chebyshev-series ((coefficient (vectorof real?)) (order natural-number?) (lower real?) (upper real?))) |
|
|
The approximations are made over the range [lower, upper] using order + 1 terms, including coefficient[0]. The series is computed using the following convention,
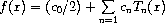
which is needed when accessing the coefficients directly.
11.2 Creation and Calculation of Chebyshev Series
Function:
(make-chebyshev-series-order order) |
|
Contract: (-> natural-number? chebyshev-series?) |
|
|
Function:
(chebyshev-series-init cs func a b) |
|
Contract: (-> chebyshev-series? procedure? real? real? void?) |
|
|
11.3 Chebyshev Series Evaluation
Function:
(chebyshev-eval cs x) |
|
Contract: (-> chebyshev-series? real? real?) |
|
|
Function:
(chebyshev-eval-n cs n x) |
|
Contract: (-> chebyshev-series? natural-number? real? real?) |
|
|
11.4 Examples
Example: The following program computes Chebyshev approximations to a step function. This is an extremely difficult approximation to make, due to the discontinuity, and was chosed as an example where approximation error is visible. For smooth functions the Chebyshev approximation converges extremely rapidly and errors would not be visible.
(require (planet "chebyshev.ss" ("williams" "science.plt"))) (require (lib "plot.ss" "plot")) (define (f x) (if (< x 0.5) .25 .75)) (define (chebyshev-example n) (let ((cs (make-chebyshev-series-order 40)) (y-values '()) (y-cs-10-values '()) (y-cs-40-values '())) (chebyshev-series-init cs f 0.0 1.0) (do ((i 0 (+ i 1))) ((= i n) (void)) (let* ((x (exact->inexact (/ i n))) (y (f x)) (y-cs-10 (chebyshev-eval-n cs 10 x)) (y-cs-40 (chebyshev-eval cs x))) ;(printf "~a ~a ~a ~a\n" ; x y y-cs-10 y-cs-40) (set! y-values (cons (vector x y) y-values)) (set! y-cs-10-values (cons (vector x y-cs-10) y-cs-10-values)) (set! y-cs-40-values (cons (vector x y-cs-40) y-cs-40-values)))) (printf "~a~n" (plot (mix (points (reverse y-values)) (points (reverse y-cs-10-values))) (x-min 0) (x-max 1) (y-min 0) (y-max 1) (title "Chebyshev Series Order 10"))) (printf "~a~n" (plot (mix (points (reverse y-values)) (points (reverse y-cs-40-values))) (x-min 0) (x-max 1) (y-min 0) (y-max 1) (title "Chebyshev Series Order 40"))))) (chebyshev-example 100)
Figures 71 and 72 show the resulting output plots.
|
|
![[chebyshev-Z-G-3.gif]](chebyshev-Z-G-3.gif)
![[chebyshev-Z-G-4.gif]](chebyshev-Z-G-4.gif)