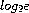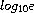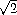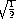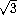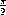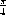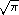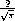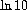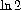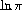Mathematical Functions
This chapter describes the basic mathematical constants and functions provided by the PLT Scheme Science Collection.
The constants and functions described in this chapter are defined in the math.ss file in the science collection and are made available using the form:
(require (planet "math.ss" ("williams" "science.plt")))
4.1 Mathematical Constants
Table 5.1 shows the mathematical constants defined by the PLT Scheme Science Collection.
4.2 Infinities and Not-a-Number
PLT Scheme provides +inf.0 (positive infinity), -inf.0 (negative infinity), +nan.0 (not a number), and -nan.0 (same as +nan.0) as inexact numerical constants. The following functions are provided as a convenience for checking for infinities and not-a-number.
Function:
(nan? x) |
|
Contract: (-> any? boolean?) |
|
|
(not (number? x)), which is true if x is not a number.
Function:
(infinite? x) |
|
Contract: (-> any? (union (integer-in -1 1) boolean?)) |
|
|
(finite? x) is not equivalent to (not (infinite? x)), since both finite? and infinite? return false for anything that is not a real number.
Function:
(finite? x) |
|
Contract: (-> any? boolean?) |
|
|
(finite? x) is not equivalent to (not (infinite? x)), since both finite? and infinite? return false for anything that is not a real number.
4.3 Elementary Functions
The following functions provide some elementary mathematical functions that are not provided by PLT Scheme.
Function:
(log1p x) |
|
Contract: (-> real? number?) |
|
|
Function:
(expm1 x) |
|
Contract: (-> real? real?) |
|
|
Function:
(hypot x y) |
|
Contract: (-> real? real? real?) |
|
|
Function:
(acosh x) |
|
Contract: (-> real? real?) |
|
|
Function:
(asinh x) |
|
Contract: (-> real? real?) |
|
|
Function:
(atanh x) |
|
Contract: (-> real? real?) |
|
|
Function:
(ldexp x e) |
|
Contract: (-> real? integer? real?) |
|
|
Function:
(frexp x) |
|
Contract: (-> real? (values real? integer?)) |
|
|
4.4 Testing the Sign of Numbers
Function:
(sign x) |
|
Contract: (-> real? (integer-in -1 1)) |
|
|
4.5 Approximate Comparisons of Real Numbers
It is sometimes useful to be able to compare two real (in particular, floating-point) numbers approximately, to allow for rounding and truncation errors. The following function implements the approximate floating-point comparison algorithm proposed by D.E. Knuth in Section 4.2.2 of Seminumerical Algorithms (3rd edition).
Function:
(fcmp x y epsilon) |
|
Contract: (-> real? real? real? (integer-in -1 1)) |
|
|
The implementation of this function is based on the package fcmp by T.C. Belding.